（本文来源：http://blog.sciencenet.cn/blog-1475614-816041.html）

生物圈中纷繁复杂的生命并不是杂乱无章的堆砌，它们形成了一种镶嵌、包蕴、相互作用以及互为因果的层次性结构：细胞→组织→器官→个体→种群→群落→生态系统→生物圈。在每个生命层次，又各具有独特的动态规律或模式，决非仅仅源自低层次的简略式叠加。如何用模型来描述一个由数百万种生物编织成（我们自身也交融于其中）的绚丽而纷杂的生态系统动态或行为呢？这是对人类认知与智慧的挑战！ 

   笔者在之前的博文：用数学统御生命世界的梦想（http://blog.sciencenet.cn/blog-1475614-812047.html）中，讨论了群落以下生命层次的数学模型，譬如种群动态的模型描述，包括单一种群和二个相互作用的种群。理论上来说，如果每个种群的行为以及种群间的相互作用都可以用数学模型精确描述的话，我们就能准确预测整个生物群落乃至整个生态系统的一切行为了。遗憾的是，这在绝大多数情况下是根本不可能的，因为一般的自然生态系统往往种类繁多，物种间的相互作用与关系极为错综复杂。即便如此，在相对整体的水平上对生态系统在一定时间尺度上的行为轨迹或动态特征的理解依然是十分重要。 

  

 

   早在一个多世纪以前，德国著名的哲学家狄尔泰（Wilhelm Dilthcy，1833—1911）试图用一种动态的生命哲学观来诠释生命的本质，认为生命是一种不能用理性概念描述的活力，是一种不可遏止的永恒的冲动，是一股转瞬即逝的流动，是一种能动的创造力量，它既井然有序，又盲目不定；既有一定方向，又不能确定。这种强烈的动态生命观充满了对立与统一的辩证哲学思想，虽然很遗憾它带上了一些非理性的唯心主义的认识观。 

 

任何生态系统结构化的生命层次—个体、种群、群落都处在不断的变化与发展过程之中，生态系统的非生物环境亦如此。但是，另一方面，任何生态系统及其不同层次也会呈现出相对的稳定特性。正如皮亚杰（1989）指出的那样，“每一种发展，无论是系谱的还是器官的，最终都会达到一种相对平衡的状态，而且，由于自动调节机制，它实际上必然如此”。从本质上来说，所有生命系统都是在稳定和变化的矛盾统一体中产生、存在与发展，而有效调节和平衡动态与稳定是所有生命系统运作的本质特征之一。超越系统调节能力的波动将导致系统状态的飞跃，或使系统走向崩溃。 

正如詹奇（1992）所说，一方面活系统连续地更新自身并不断地调节这个过程以保持其结构的整合性，而另一方面活结构又不可能无期限的保持稳定。如果按控制论的话来说，生命系统通过负反馈机制维持结构的相对稳定性，通过正反馈机制失稳而发展出新的模式或走向崩溃。这就是说，生命系统具有一定的自组织性与自我调节性，还能通过过程的相互作用推动结构的演化。但事实上，在大多数情况下，我们对自然生态系统中存在的这种正负反馈机制的认识还是相当有限的，因为许多生态系统的结构以及组分间的相互关系过于复杂，难以进行准确的定量描述。但是，关于生命系统宏观状态与行为的趋势性分析依然是可行的并具有一定价值的。 

本文拟从稳定性、可塑性和稳态转化透视生态系统的状态与行为，虽然对稳定性、可塑性及稳态转化等只能进行定性—半定量的研究，而且主要涉及一些生态学上中等时间尺度（数十年）的过程，但是一些却与人类对生态系统的管理息息相关，因为这正好位于或接近于人类易于感知以及可能操控的时间尺度。 

 

  

一、对稳定性的认识—从种群到生态系统 

1.稳定性—涉及生态系统的各个层面 

稳定性是一个在所有学科都广泛使用的词汇，特别是关于各种系统（生命的或非生命的）状态的稳定性，如自动控制系统的稳定性、农业生态系统的稳定性，等等。 

在生态学领域，人们常常在生态系统的不同层次谈论稳定性，譬如，“种群稳定性”、“群落稳定性”、“系统稳定性”、“生态功能稳定性”，也有人简称“生态稳定性”，环境也有“稳定性环境”或“非稳定性环境”之说。 

就如同人们在不同的时空尺度使用生态系统、生物群落和种群一样，人们也常常在不同的时空尺度谈论稳定性问题，因此就可能有诸如“长期稳定性”之类的说法，但在生态学领域，多数研究主要涉及中小时空尺度的稳定性问题。 

良性生态系统稳定性的维持机制一直都是应用生态学家关注的重要问题之一，因为只有阐明了稳定性的机制，才有可能在生产或保护实践中维持或调控目标生态系统的稳定存在或发展。关于稳定性的机制，人们特别关注多样性或复杂性与稳定性之间的关系。 

2.认识发展的几个关键节点 

20世纪50年代，以MacArthur（1955）为代表的生态学家试图构建与种群间相互作用（如捕食者—被捕食者）为核心的生态稳定性理论，主要是在种群和群落水平。20世纪70年代初，人们对生态系统的认识（虽然也还是基于捕食者—被捕食者这样较简单系统的分析）从单一的平衡状态到多个平衡状态的转变（Holling 1973），宣告了理论生态学家的杰作—生态可塑性概念的粉墨登场。20世纪90年代初，以Scheffer为代表的生态学家（Scheffer et al. 1990）开始以水生态系统（特别是湖泊生态系统）为例，研究生态系统在不同状态间的转化问题（即所谓稳态转化），这或许因为湖泊生态系统（特别是浅水湖泊）在人类活动的干扰（如营养盐输入）下，在较短的时间尺度（数年至数十年），出现明显的状态（如浊水—清水）转化。 

  

二、种群和群落稳定性—概念与度量 

1.什么叫做“种群稳定性”和“群落稳定性”？ 

MacArthur于1955年在Ecology的论文“动物种群的波动，及群落稳定性的度量”堪称关于稳定性的经典之作，该文给“种群稳定性”和“群落稳定性”下了简单而直观的定义：种群稳定性—“在一些生物群落，物种丰度趋于十分稳定，而在另一些群落，物种丰度变化很大，将前者称为稳定，后者称为不稳定”；群落稳定性—“在一些生物群落，……，由于一些原因，一个物种异常增殖，如果另外种类的丰度由于前者而显著变化，则称群落不稳定，如果异常增殖的物种对其它物种的影响越小，群落就越稳定”。 

MacArthur的群落稳定性定义虽简单，但到底指什么还是不甚明确，譬如“对群落中其它种的影响”可以有多种不同的解读，它可能指平均（所有种）最大丰度变化，或者指相对变化、或者指平均平方变化，或者不同的种类能被不同的权重等。 

此外，如果从生态对策的角度来审视种群的稳定性问题，还是挺有意义的。一般来说，个体大、繁殖速度慢的K-对策物种的种群稳定性较好，而个体小、繁殖速度快的r-对策物种的种群稳定性较差。因此，K-对策物种是对所谓“稳定性环境”的一种适应，而r-对策物种是对所谓“非稳定性环境”的一种适应。这不仅在解释短期的种群行为或许在解释地质环境变化过程中不同生态对策物种的进化上也会具有意义。 

2.种群和群落稳定性的概念—动听却难以度量 

   如何度量种群稳定性？依据MacArthur的定义似乎难以对种群稳定性进行严格的度量。也许可以考虑两种度量办法：1）对大小完全不同的物种，用内禀增长率r的大小或许可以判断稳定性的大小；2）对于大小和繁殖率相近的物种，也许可以用比较种群波动的振幅、频率的大小或者震荡的不规则性来进行度量。直观地说，振幅越大、频率越高、震荡越不规则，则种群越不稳定。 

   如何度量群落稳定性就更为困难了。人们常常将食物网的复杂程度（如能量流动途径或食物链结点数）与群落稳定性直观地联系起来，即直观地（当然也是基于一定的经验）认为能量在食物网中流动的途径越多，群落稳定性越大（Odum 1953）。MacArthur（1955）运用绵密的逻辑分析力图证实这一观点的合理性。 

MacArthur首先通过对种群丰度的二种极端情形的定性分析试图说明其推论的合理性，即一种情形是一个群落中某一物种的种群异常的大，为了减少其对群落中其它种群的影响，必须有大量的捕食者去分散过剩的能量，该物种必须有大量的饵料种群不至于使种群减少太多，也就是说，通过每个物种的多种（能量流动）途径的存在是减少一个种类的种群过剩效应所必须；另一种情形是一个群落中某一物种的种群异常的小，为了将其对群落中其它种群的影响减少到最小，该种的每一种捕食者应该有大量的可替代食物以减少对稀有种的压力，同时也能将其自身的种群丰度维持在与原来非常接近的水平。因此，这二种情形中的任一种都表明通过食物网的可选择能量流动途径的多寡度量了稳定性。 

接下来，MacArthur依据对生态现象的经验性观察，直觉地赋予了群落稳定性若干特性：1）稳定性随食物链结点（link）增加而增加，直觉上似乎是如果一个物种仅有一种捕食者和一种食物（饵料），其稳定性应该最小；2）如果每个物种的饵料物种数目一定，群落中物种数的增加将增加稳定性；3）一定程度的稳定性可通过大量的物种（每种的食物相当局限）或通过少量的物种每种捕食许多其它物种来实现；4）对一个有m个物种的群落，但有m个营养级且每个物种捕食其下面的所有物种时，稳定性将达到最大，如果一个物种捕食其它所有种类且这些种类全在一个营养级时，稳定性将达到最小。因此，食谱变窄将降低稳定性，但却是效率所必须，二者都是在自然选择压力下生存所需要的特性，自然选择可能使动物在保证必要的稳定性条件下使效率达到最大化。 

最后，MacArthur用上述赋予的特性，试图解释北极和热带地区的群落稳定性问题：1）在物种稀少的北极地区，很难或不可能获得稳定的食物供给，猎食者不得不捕食广泛的食物种类，也能期待见到许多营养级（相对于物种数而言），即便如此，也难以保证稳定性，因此在北极地区，种群容易剧烈波动；2）而在物种丰富的热带地区，即便是十分狭窄的食谱也能获得所需的稳定性，物种能沿着特定的线路特化，营养级可能相对较少（相对于物种数而言）。 

MacArthur的观点虽被广泛引用，但是无论是关于种群还是群落稳定性，都无法进行定量的度量，主要局限于为人们提供对种群和群落稳定性进行精神思辨的食粮。 

  

三、系统稳定性—概念与度量 

1.用简单的系统诠释复杂的系统稳定性 

Holling（1973）从纯理论的角度研究了一个非常简单的系统（只有二个种群组成）的行为。二个相互作用的种群可以是捕食者—被捕食者，或牧食动物—被牧食植物或二个竞争者。他图示了如何用相平面来刻画二个种群之间相互作用的轨迹。相平面概念是Poincare H 于 1885 年首先提出来的，是求解一、二阶线性或非线性系统的一种图解法，常用来分析系统的稳定性。 

 

 

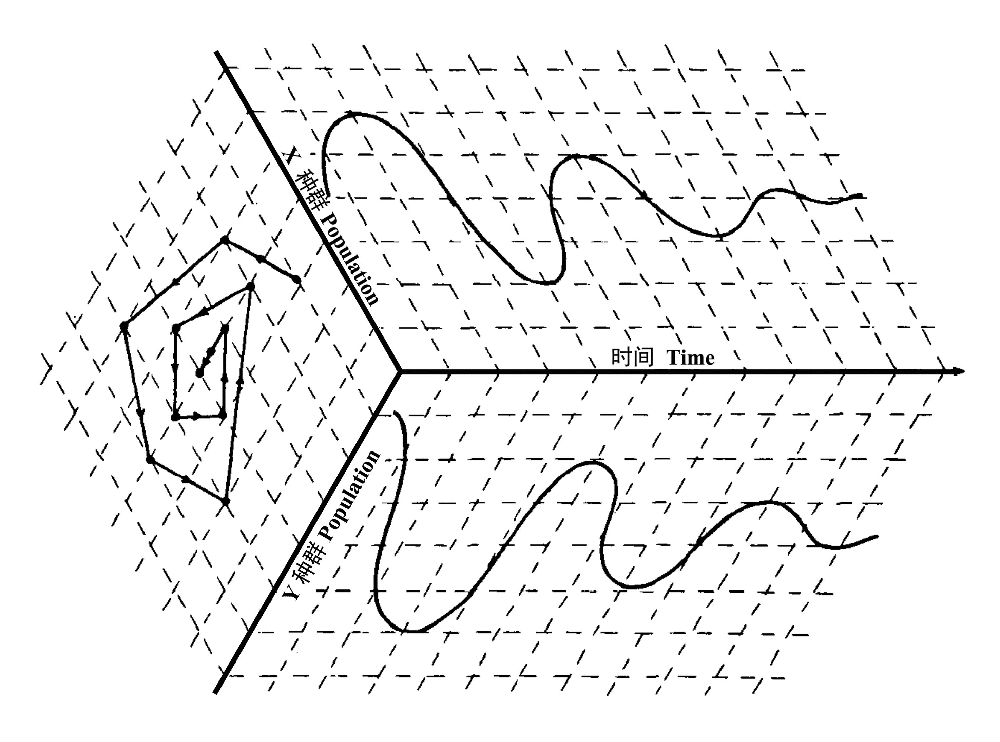
图1 二个种群数量的时间变化导出的相平面（引自Holling 1973） 

  

设想在一个恒定环境中向一个或二个种群施加的扰动将导致种群波动，其振幅将逐渐减小，这可用图1来表示，这里每个种群的时间波动显示在盒子的侧面。在这个例中，二个种群在某种意义上是相互调控的，但是滞后响应导致了一系列的振动，其每个种群的振幅逐渐减小到一个恒定的值。但是，如果我们也关心持续性（persistence），那我们将不仅想知道这二个种群是如何从特定的一对初始值开始其行为轨迹，而且想知道所有可能的成对值，因为也许就存在若干个初始种群组合可导致二个种群中的一个或另一个灭亡。但是，在时间轴上显示可能响应的全部变化是非常困难的，而在相平面上绘出轨迹被证明是方便的，如图1盒子底部所示，这里的二个轴表示二个种群的密度。在平面上的轨迹表示在一定的时间间隔二个种群序列的变化，每个点表示每个种群在特定时间点的特有的密度，箭头表明时间变化的方向。如果振动衰减，如显示的例子，该轨迹将呈现一个封闭的螺旋，最终达到一个稳定的平衡。 

接下来，Holling描述了相平面中各种不同形式的轨迹，并定义了各种各样的数学或系统学上的稳定性概念：图2A为一个开放的螺旋，表示波动的振幅逐渐增加，添加的小箭头暗示无论何种种群组合来启动轨迹都是这样的结局；图2B的轨迹是封闭的，任何出发点都会回到那一点，尤其重要的是每个出发点都产生一个独特的环，这些点不倾向于汇集到一个单一的环或点去，这也称为中性稳定性（neutral stability），这是一个理想的无摩擦的摆钟显示的稳定性；图2C显示的是一个与图1类似的稳定系统，这里相平面中所有可能的轨迹都螺旋进一个平衡。这三个例子都相对简单，但与经典的稳定性分析有关，也可能正是生态学的理论好奇之处。 

图2D～2F增加了一些复杂性，在某种意义上，图2D是A和C的组合，在相平面的中央，所有可能的轨迹都向内螺旋进平衡，而在这个区域外的都向外螺旋，最终导致的一个或另一个灭绝。这与图2C的全域稳定性（global stability）相反，是一个局域稳定性（local stabilty）的例子。他指定表现稳定性的区域为吸引域（domain of attraction），包含该域的线为吸引域的边界（boundary）。图2E的行为正好相反，在一个内部的区域，轨迹向外螺旋至一个稳定极限环（a stable limit cycle），如果越过了该环，轨迹再向内接近它。最后，图2F显示一个稳定节（stable node），此时无震荡，轨迹单调地接近节点。这六种图形能以几乎无限变化方式组合产生若干吸引域，在其中能见到稳定平衡、稳定极限环、稳定节点或中性稳定轨道。 

Holling认为，这之前的传统模型的行为特点是1）要么是全域稳定或者是全域不稳定，2）中性稳定性非常不可能，以及3）当模型稳定时，极限环就是一个可能的结果。 

 

 

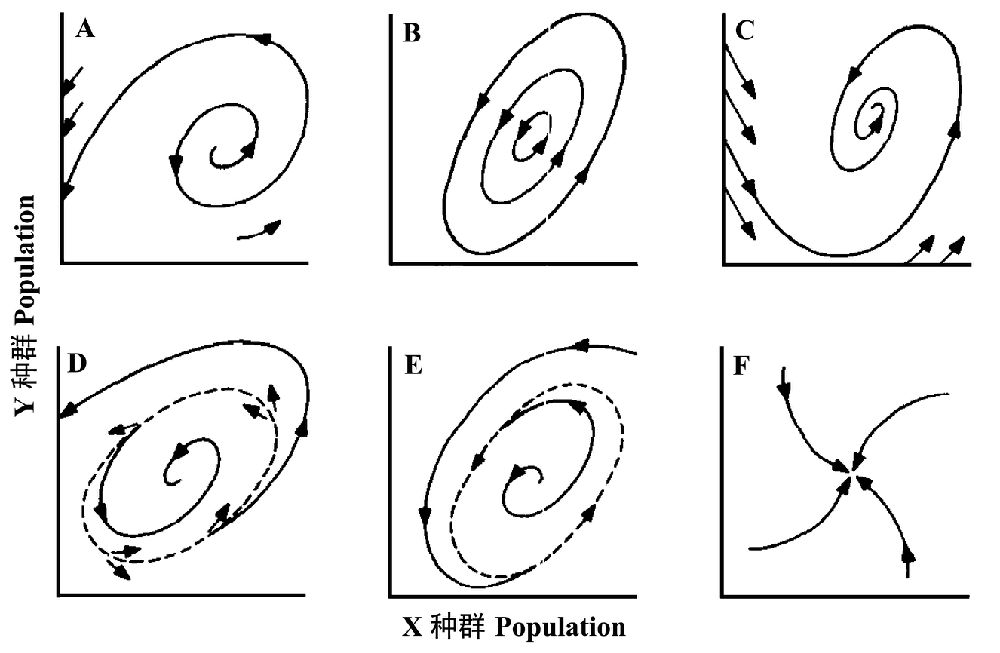
图2 相平面中系统可能的行为案例，（A）非稳定的平衡，（B）中性稳定平衡，（C）稳定平衡，（D）吸引域，（E）稳定极限环，（F）稳定节点（引自Holling 1973） 

  

   Holling形象地可用一个钵（bowl）来表示势能场（potential field）（图3），如果整个势能场为一个浅钵，系统将为全域稳定，所有轨迹将旋向钵底—平衡点；但如果至少有一个较低的（如猎物）灭绝阈值，钵的一边将撕开一个裂口（如图3），如果轨迹启动位置过高的话，较大的振幅将携带其超越该裂口，而只有那些正好避开了裂口最低点的轨迹才能旋进钵底。可将钵称为吸引盆（basin of attraction），那么吸引域（domain of attraction）将由周期性行为和力的构型所决定。 

  

 

 

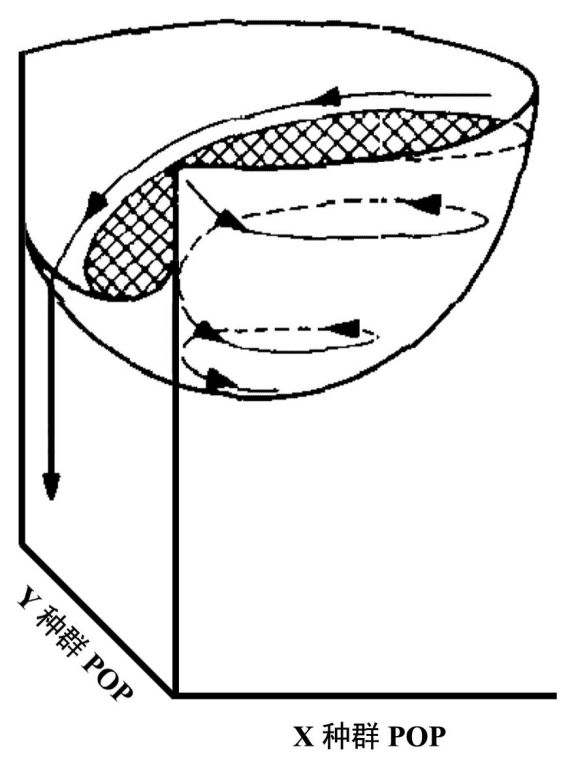
图3 轨迹在势场上移动的反馈力的略图，阴影部分表示吸引场（引自Holling 1973） 

  

2.大胆的外延—提出从单个到多个平衡状态的新的系统观 

Holling（1973）认为传统的系统观仅聚焦于系统在某个平衡点附近的行为，而忽略了系统可能在多个平衡状态间的转换：仅关注个体死亡、种群消失和物种灭绝，譬如在一些年份猫头鹰多、老鼠少，而在另外的年份，情况相反；又如鱼类种群随自然条件有盛有衰；再如昆虫种群极端变化到只有对数转换才容易表示；此外，在不同的区域，经过或长或短的时间，物种能完全消失，然后又再现。 

Holling认为，传统的系统观更多的是直观的和表象的，科学的系统观不应该只关注有机体数量的多寡及它们数量的恒定程度，因为一个原始（未被扰动）的生态系统在自然历史进化的长河中可能经历了多个不同的平衡状态，在人类活动（资源利用、污染等）的影响下，生态系统可能从一个平衡状态转变（退变）到另一个平衡，常常导致严重的生态后果（如物种濒危甚至消失）。因此，科学的系统观应聚焦于并充分认识多平衡状态及其邻域条件，从这种角度来审视生态系统的行为将可能获得不同但有用的见解，而基于上述二种不同世界观的策略可能恰好是对立的。 

在这里，笔者不得不感叹的是理论生态学家借用相平面图以及用仅有2个种（这比任何一个自然生态系统都简单得不能再简单的了）的相互作用的理论轨迹勾勒出了系统稳定性的框架，并大胆地扩展到谈论生态系统的稳定性问题。简单地说，Holling（1973）用这种巧妙的手法，试图让人们相信复杂的自然生态系统中也存在多稳定域（multiple stability domains）或多吸引域（multiple basins of attraction），以及它们是如何与时空尺度下的生态过程、随机事件（如干扰）和异质性相关联的。 

3.系统稳定性的度量—一样困难 

与种群和群落稳定性的度量一样，系统稳定性的度量也是一件极其困难之事。Pimm（1991）认为，一个系统当且仅当所有的变量在扰动后都返回了最初的平衡才被认为是稳定的，如果这仅适用于小干扰，则系统为局域稳定（locally stable），如果系统能从所有可能的干扰均能返回，称为全域稳定（globally stable），系统返回特定平衡相关的变量的所有数值的集合称为吸引域，稳定性是无量纲的（non-dimensional），二进制的，0表示不稳定，1表示稳定。 

Gallopin（2006）认为，常用的稳定性概念聚焦平衡点或轨迹附近系统的行为，可通过干扰后系统返回稳定点或轨迹的速度来度量，这本质上就是Pimm（1984）定义的可塑性概念，后来被Holling（1996）称之为工程可塑性，这也相等于在数学里熟知的局部稳定性概念。 

迄今为止，还是没有一个大家普遍接受的系统稳定性的度量方法，还只是停留在定性的描述而已。这可能是由于上述系统稳定性概念来源于理论生态学家对非常简单的生态系统（仅由二个物种组成）的抽象，而一个复杂的生态系统（如热带雨林）则可能由成千上万个物种错综复杂地相互联系与交织在一起，二者相差甚远，而且理论生态学家也没有对所涉及的生态系统的时空尺度予以界定。即便如此，生态系统的多稳定状态是现实存在的，从理论生态学角度提出的系统稳定性概念依然具有重要价值。 

4.稳定性景观—形象地描绘多稳态系统 

一些学者还试图通过形象的方式表示一个含有多个稳态的系统，将系统的多个稳定状态抽象地图示在一起，称之为“稳定性景观（stability landscape）”，这是一种直观地描绘系统的动态特征（包括各稳态之间的相互关系）的手法，这里的景观类似于景观生态学中景观的含义，但它纯粹是抽象的。 

Gallopin（2006）图示了具有3个域的1个系统，A域含有一个稳态（steady state），B域含有一个稳定圈（stable cycle），C域含有一个稳定轨迹（stable trajectory）；整个图描绘了系统的“稳定性景观”，由所有吸引域的构型所表征，包括区分它们的边界；稳定性景观格局是系统结构的一部分，依赖于系统的参数赋值（固定的或非常缓慢变化的因素）（图4）。在一个拥有多个吸引子的动态系统，一些关键参数的连续变化能导致系统稳定性景观的不连续变化（图5），这些不连续体（discontinuities）在动态系统数学理论中称为分叉（bifurcations），在灾害理论中称为灾变（catastrophes）。 

需要指出的是，稳定性景观依然是一种描述性的概念模式，还无法定量化，因此也只是一种理论生态学家对系统稳定性的形象思考。 

 

 

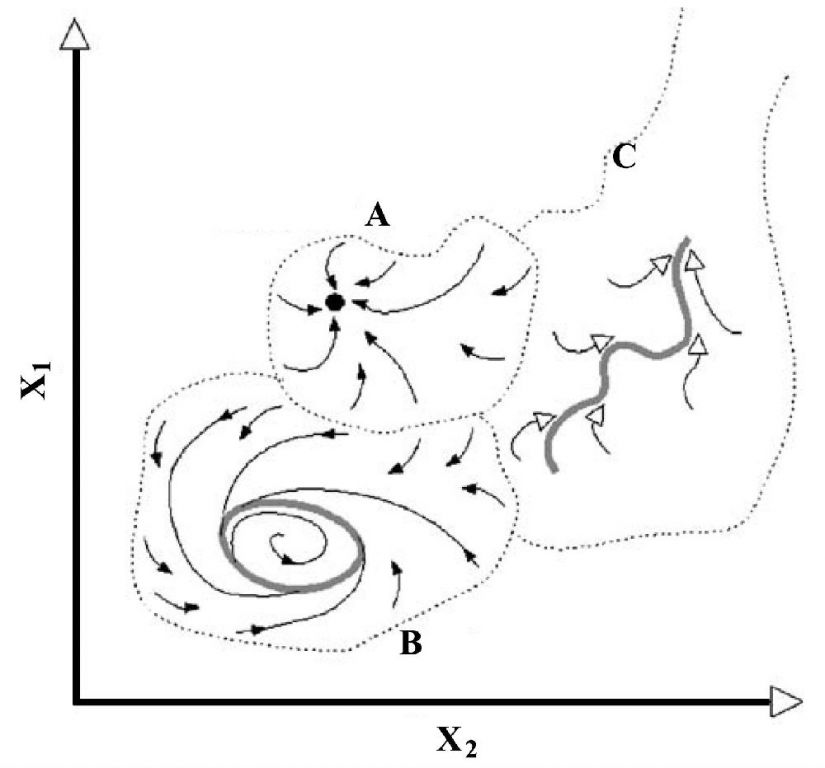
图4 拥有2个变量（X₁、X₂）3个吸引子（A、B、C）的状态空间，虚线表示各自的吸引域（引自Gallopin 2006） 

  

 

 

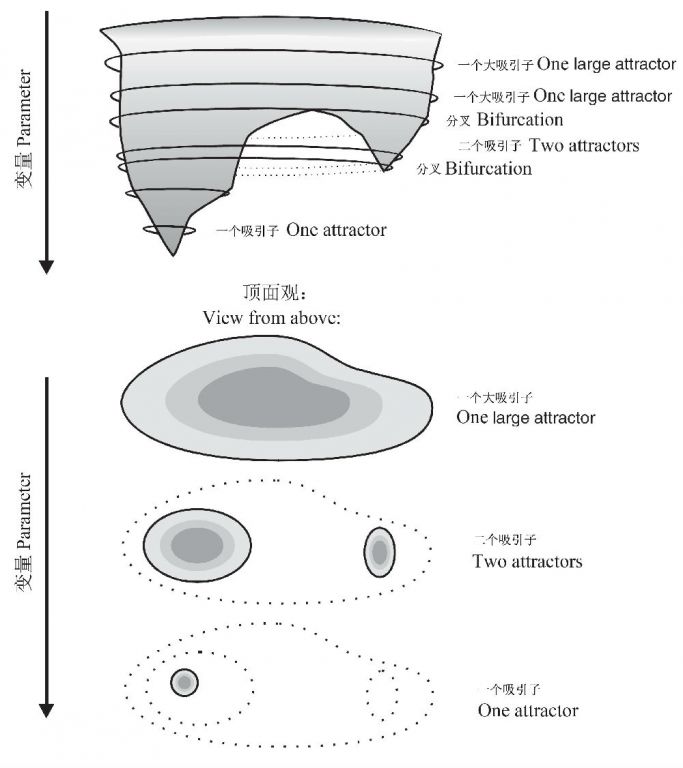
图5 吸引子的定性变化。1个参数的连续变化能引起吸引子萎缩、分裂或消失。上图是三维的表示，下图是顶面观，立体图形的3个剖面（引自Gallopin2006） 

  

四、生态功能稳定性模型 

凭借经验和直觉，一些学者认为一个生态系统中存在的物种越多，物种间的相互作用就会越复杂，生态功能（Stability of ecological function）也应该更为多样和稳定（Peterson et al. 1998）。我感到有些疑惑的是，这里的生态功能稳定性所指含糊，不知是指生态系统的物质循环和能量流动的稳定性，还是指种群、群落或生态系统的稳定性。 

物种多样性增加生态（功能）稳定性的直观思想最早由达尔文提出（Darwin 1859），然后被MacArthur（1955）再描述，后来被May（1973）模型化。Peterson等（1998）将描述物种多样性增加导致生态功能稳定性增加的竞争性模型（competing models）分为四类：物种多样性模型、异质性模型、“铆钉”模型和“驾驶员和乘客”模型。 

1.物种多样性模型 

达尔文（1859）曾经提出，一个被大量物种占居的区域比一个被少量物种占据的区域更具有生态稳定性。Peterson等（1998）将这一思想进行概念性模型化（图6），认为随着物种的累积，它们占居多维生态功能空间（插图的宽度和高度表示一个物种生态功能的宽度和强度），该模型假设功能空间相对较空，因此物种能被不断地加入到群落中去而不饱和，并假设生态功能的强度和宽度不随物种的不同而变化。 

 

 

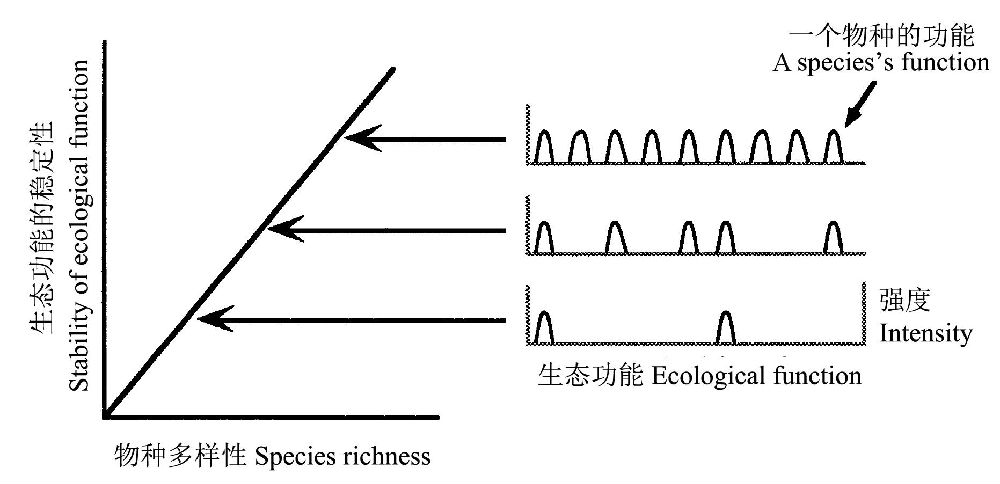
图6 Darwin/MacArthur模型的图示：物种丰度的增加使生态功能的稳定性增加（引自Peterson et al. 1998） 

  

2.异质性模型 

异质性模型（idiosyncratic model）（图7）主张每个物种对生态功能的贡献受物种之间相互关系的强烈影响，因此，向（从）生态系统中引入（移出）物种的影响根据引入（移出）物种的性质以及与其相互作用的物种的性质的不同表现得或者不显著或者严重（Peterson et al. 1998）。譬如，红火蚁对美国东南部生态系统有很大影响（Porter and Savignano 1990; Allen et al.1995），但在其原产地巴西和巴拉圭的沼泽中却有着非常不同功能（Orr et al. 1995）。 

当然，生态系统的功能虽依赖于区域中相互作用的生物物种的生态与进化历史，但也不仅仅是历史事件的产物，许多生态系统虽然拥有很不相同的生物群落，但却被组织成行使相似的生态功能（Peterson et al. 1998）。譬如，在世界五大地中海气候区，虽然由于地理和进化的隔离形成了完全不同的动植物区系，但生态结构和功能却极为相似（Di Castri and Mooney 1973；Kalin Arroyo et al. 1995）。 

 

 

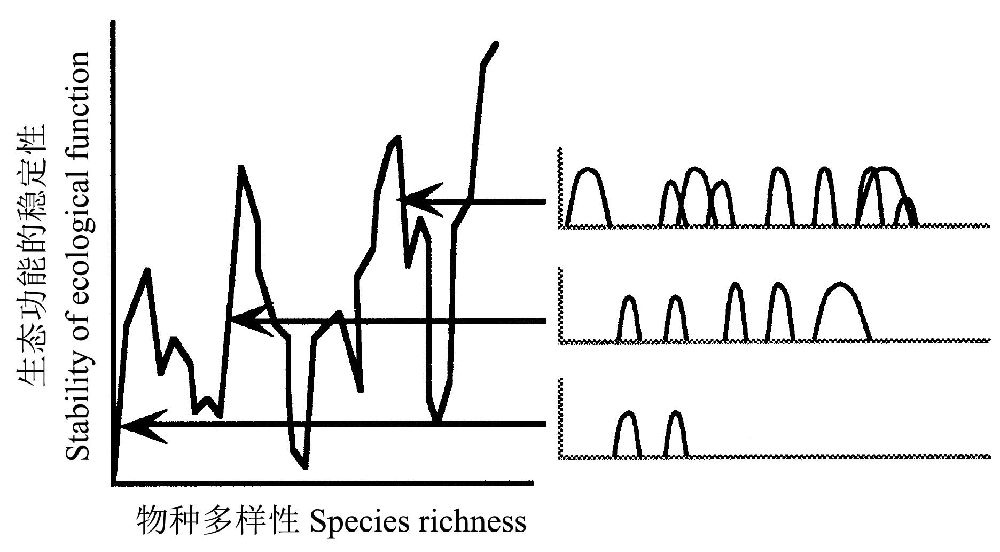
图7 异质性模型（Lawton 1994）的图示：生态功能随着物种丰度的增加而呈现异质性变化（引自Peterson et al. 1998） 

  

3.“铆钉”模型 

大量经验事实表明物种移出或引入一个生态系统的影响会不尽相同。Ehrlich and Ehrlich（1981）提出了所谓“铆钉”模型（“rivet” model），将生态功能比喻为机翼上的“铆钉”，在机翼脱落之前可以失掉几颗铆钉。该模型假设生态功能的空间相对较小，因此，一个物种加入到生态系统，其功能开始重叠或相互间互补。虽然少数种类丧失了，但是这种重叠使生态功能得以持续，因为具有相似功能的物种能够补偿其它物种的去除或下降所产生的影响。但是，通过新物种的引入获得的稳定性增加将随着物种的增加及功能空间的不断拥挤而下降（图8）。 

 

 

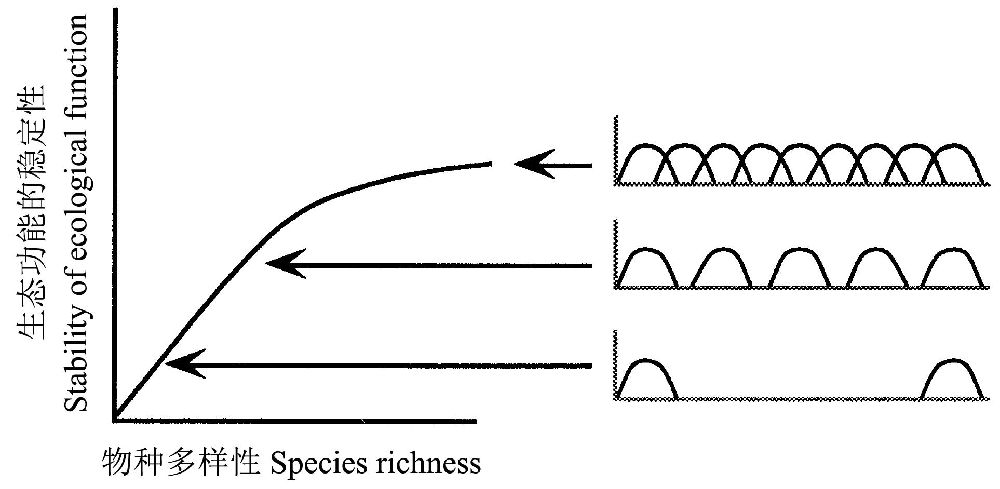
图8 Ehrlich和Ehrlich（1981）提出的“铆钉”模型的图示（引自Peterson et al. 1998） 

  

4.“驾驶员和乘客”模型 

Walker（1992，1995）提出了所谓“驾驶员和乘客”模型（‘‘drivers and passengers’’ model）（图9），认为生态功能依赖于“驾驶员”物种或其功能性类群，即“驾驶员”物种具有强烈的生态功能，显著影响其自身及“乘客”物种所在的生态系统的结构，而“乘客”物种的生态功能很小。“驾驶员”物种能有各种形式，它们可能是生态工程师（ecological engineers），譬如海狸或地鼠陆龟塑造物理环境（Diemer 1986，Jones et al. 1994，Naiman et al. 1994），或者它们可能是“关键物种（keystone species）”（Paine 1969），譬如与其他物种有着强烈关系的海獭或非同步成熟的果树（Terborgh 1986, Estesand Duggins 1995, Power et al. 1996）。“驾驶员”物种的存在与缺失决定生态系统功能的稳定性（Walker 1995）。 

 

 

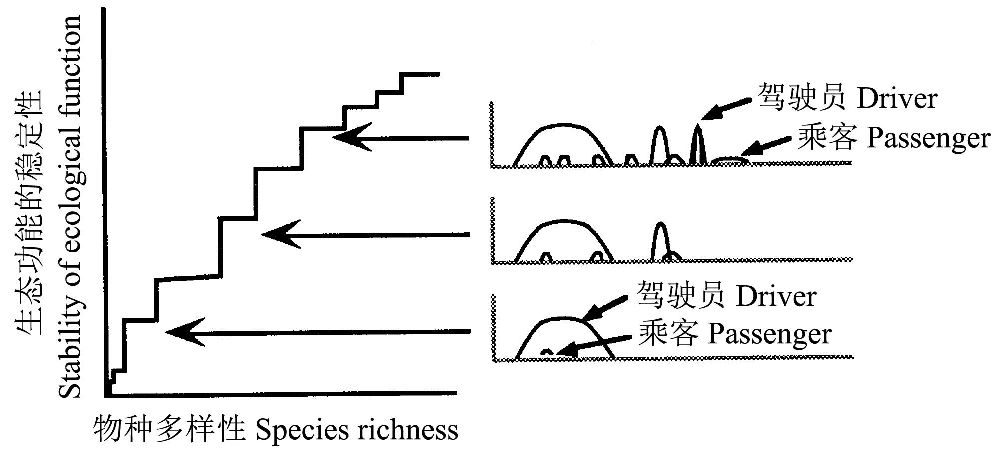
图9 Walker（1992，1995）的关于冗余生态功能的“驾驶员和乘客”模型假设生态功能在物种间非均匀地分布。“驾驶员”物种的生态影响大，而“乘客”物种的生态功能极小。“驾驶员”物种的加入增加系统的稳定性，而乘客物种的影响极小或没有（引自Peterson et al. 1998） 

  

5.模型整合 

   Peterson等（1998）认为一个能最好地描述生态系统的模型依赖于该生态系统中生态功能的分化程度以及物种间生态功能分布的均匀度：如果一个生态系统中的构成物种每一种都行使不同的功能，而另一种生态系统具有同样数目的物种但每个物种有广泛的生态功能，那么前者比后者的冗余要少；同样，如果不同物种之间的生态影响几乎没有差别，就分不出“驾驶员”和“乘客”，因此就适合用“铆钉模型”。他们将物种多样性如何影响生态功能稳定性的几个模型整合到一个简单的模型中，横轴为物种间生态功能的重叠程度，纵轴为物种间生态功能的变化程度（图10）。 

 

 

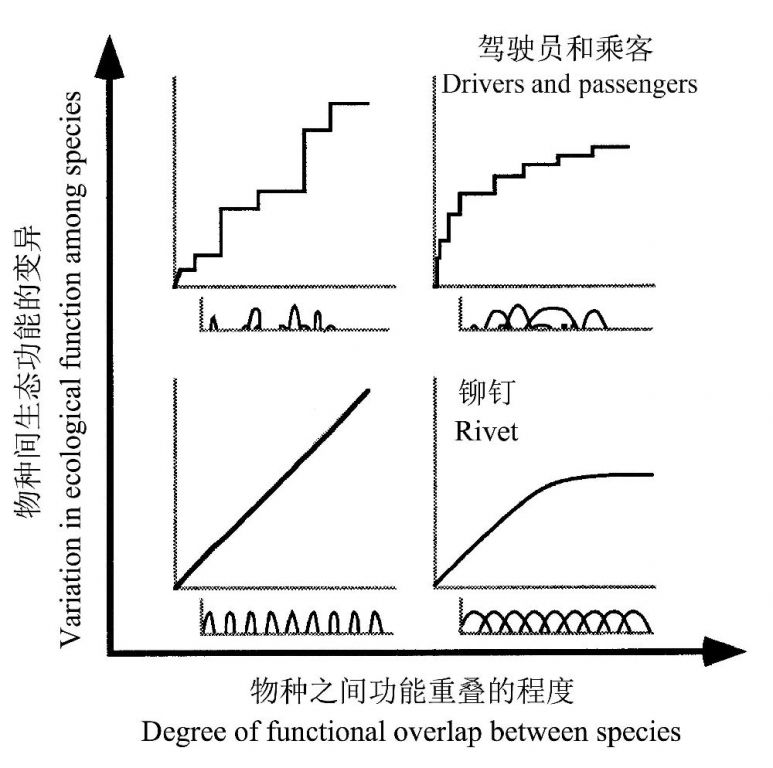
图10 物种多样性和稳定性之间的关系随不同物种的生态功能之间的重叠程度以及物种生态功能的生态影响的变化量而异。生态功能的重叠导致生态冗余。如果不同物种的生态影响相似，它们就是“铆钉”，如果一些种类的生态影响相对较大，它们就是“驾驶员”，而其它就是“乘客”（引自Peterson et al. 1998） 

  

上述四种模型的差异主要在如何评估物种的生态功能的多少上，其共同的基本逻辑是：1）生态功能的多少与生态功能稳定性正相关，而2）生态功能的多少又与物种（或关键物种）的数目正相关。因此，物种数越多，生态功能越稳定。这在本质上与MacArthur（1955）的观点并无多大差异，只不过关键词一个是“生态功能稳定性”，另一个是“生物群落的稳定性”。需要指出的是，上述生态功能稳定性模型也基本上是一种定性的形象化的概念性表述。当然，它们是基于不同生态系统特性的一种稳定性抽象，在引领我们对生态稳定性的思辨上仍然具有重要价值。 

  

五、生态可塑性—稳定不一定可塑，不稳定不一定不可塑 

1.生态可塑性—一种新的多平衡态的系统观 

20世纪70年代以前，理论生态学家十分关注与生态稳定理论相关的种群间（如捕食者和被捕食者）的相互作用及功能响应（Folke 2006）。Holling（1973）在其经典之作—“生态系统的可塑性和稳定性”一文中，通过经验研究、数学模型和生态系统管理经验等的分析，正式提出了生态系统可塑性的概念，将可塑性定义为“系统维持能力以及吸收变化和干扰后仍然保持种群间或状态变量间同样关系的能力的一种度量（A measure of the persistence of systems andof their ability to absorb change and disturbance and still maintain the samerelationships between populations or state variables）”。 

Holling展示了一种新的多平衡观点，认为许多自然的未受干扰的生态系统也常常处于若干稳定的暂态（transient states），它们有使系统变量趋于保留的2个或更多的吸引域，在每个域内，系统状态可能宽幅震荡（如可能高度不稳定），但如果它趋向于停留在域的边界内，系统就是可塑的。因此，可塑性意指一个多稳态系统面对干扰其状态变量在某个给定吸引域内保持的能力，而不关心状态在域内的稳定性或恒定性，生态可塑性可用导致系统状态偏移到吸引域外之前系统所能吸收的干扰量来度量（Gallopin 2006）。 

2.“五花八门”的生态可塑性定义 

Pimm（1991）将可塑性定义为“变量经过干扰后回复到其平衡状态有多快”，单位为时间。他认为可塑性因此不能针对不稳定系统，特征的返回时间为经历干扰后回复到初始值的1/e（约37%）（How fast the variables return towards their equilibriumfollowing a perturbation. Resilience is not, therefore, defined for unstablesystem. Characteristic return time is time taken for a perturbation to returnto 1/e (～37%) of initial value）。Holling（1996）认为统治着主流生态学的单一平衡观点（single equilibrium view）导致了将可塑性解释为干扰后的返回时间，并称之为“工程可塑性（engineering resilience）”。工程可塑性聚焦在稳定平衡（stable equilibrium）附近的行为及一个系统经历干扰后趋向稳态（steady state）的速率，即返回平衡的速度（Folke2006）。 

自Holling（1973）以来，许多学者对可塑性的描述或再定义，基本上大同小异（表1）。譬如，Walker等（2004）将可塑性定义为“一个系统吸收干扰、经历变化的同时重新组织以便仍然保持必需的同样的功能、结构、特性及反馈的能力（Resilience is the capacity of a system toabsorb disturbance and reorganize while undergoing change so as to still retainessentially the same function, structure, identity, and feedbacks）”。这里，生态系统的重新组织其实是生态系统的基本特性之一。 

生态可塑性的概念还被引入社会经济系统或生态—社会复合系统（表1）。Hughes等（2005）认为在认识到扰动和变化是复杂的社会生态系统不可或缺的组分的基础上，生态社会可塑性聚焦于周期性扰动、以及应对不确定性和危险性。 

  

表1关于可塑性的各种定义 

类别	定义	文献
生态的
1	系统维持能力以及吸收变化和干扰后仍然保持种群间或状态变量间同样关系的能力的一种度量	Holling 1973
2	系统通过改变变量及控制行为的过程来改变其结构前所能吸收的干扰量	Gunderson and Holling 2002
3	系统经历冲击但本质上仍然保留同样的功能、结构与反馈、（因此）统一性的能力	Walker et al. 2006
4	1）吸收干扰的能力，2）自我组织的能力，3）学习和适应的能力	Walker et al. 2002
5	提出了可塑性的四个特性：1）宽容度（吸引域的宽度），2）阻力（吸引域的高度），3）不稳定性，4）跨尺度关系	Folke et al. 2004
6	随生态系统动态而变化、发生在生态系统层次体系的每一个水平的数量特性	Holling 2001
7	可塑性指一个社会生态系统在转移到一个状态空间的不同的域（被一组不同的过程所控制）之前所能忍受的干扰量。但是，到底如何针对特定的社会生态系统去定量可塑性的大小？	Carpenter et al. 2001
8	系统在面临内部变化和外界冲击的情况下维持其同一性的能力	Cumming et al. 2005
社会—生态的
1	群体或群落通过社会、政治和环境变化应对外来压力或干扰的能力	Adger 2000
2	通过决策者的消费和生产活动在状态之间变革的可能性	Brock et al. 2002
3	系统承受市场或环境的冲击但不失去有效配置资源的能力	Perrings 2006
4	一个生态系统在面临波动的环境和人类利用的情况下维持期待的生态系统功能的根本能力	Folke et al. 2002
5	一个社会生态系统吸收周期性扰动的能力（…）以维持必须的结构、过程和反馈	Adger et al. 2005:
6	一种分析社会—生态系统的思考方法或途径	Folke 2006
7	长时期的柔韧性	Pickett et al. 2004
8	自然资源的长期维持	Ott and Döring 2004

（修改自Brand and Jax 2007） 

  

3.稳定性包含于“可塑性”之中 

Gallopin（2006）针对稳定性景观，将稳定性区分成三种类型或水平，并指出了与可塑性的关系。第一种，局域稳定性或工程可塑性，指在给定吸引域内在一个吸引子附近的系统轨迹行为；第二种，指系统状态在系统稳定性景观内不同吸引域之间的变化，系统保持在同一吸引域内的能力称为生态可塑性；第三种包括稳定性景观自身的变化，这是动力系统结构稳定性域，即系统在其动态方程被干扰情况下维护其轨迹的拓扑的能力（其稳定性景观格局的定性特征）。结构的不稳定代表原来的系统可能真正转变为不同的系统。 

Peterson等（1998）基于生态功能稳定性模型，诠释了稳定性—工程可塑性—可塑性三者之间的关系，图11A为物种多样性与生态功能稳定性模型，图11B为稳定性景观。形象地说，重力将球向下吸引，因此景观表面的凹陷处为稳定状态，凹陷越深，越稳定，因为需要不断增强的扰动才能将生态系统的状态从凹陷底部移出来。凹陷侧边的陡峭程度与维持生态系统在稳定状态附近的负反馈力的强度相对应，其结果是凹陷侧边的坡度越大，工程可塑性越大。物种越丰富，凹陷越深，即可塑性越大。 

 

 

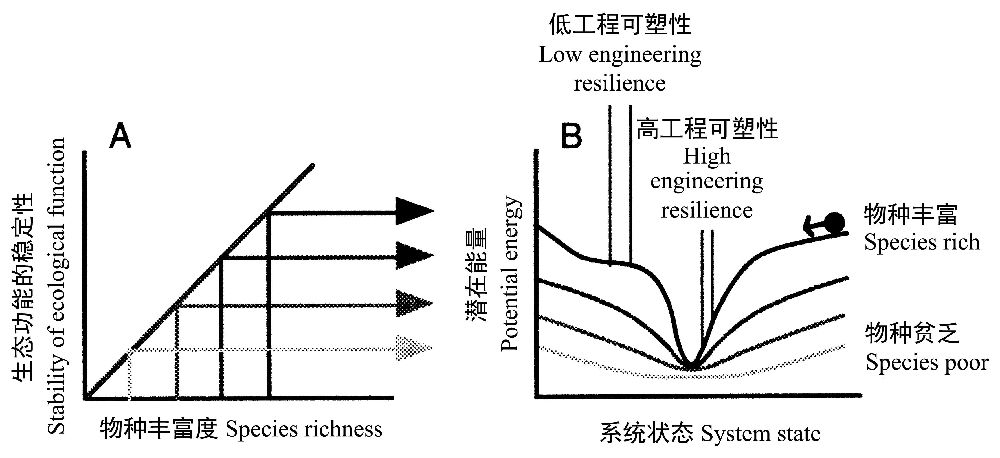
图11 稳定性和物种多样性之间的关系可用一组稳定性景观表示。一个系统的动态用一个景观表示，它的状态用一个被吸引到凹陷的球所表示。在不同的物种多样性水平可能存在不同的景观地貌。在这个模型中，凹陷越深，状态的稳定性越大。坡度较小的稳定性表面区域的工程可塑性比坡度较大的区域要小（引自Peterson et al. 1998） 

  

   假设一个生态系统能在多个自组织或稳定的状态之间切换，则生态可塑性就是使系统从一种状态转移到另一种状态所需要变化的度量（图4-12）。一个状态的稳定性是一个局部的测度，而一个状态的可塑性是一个更大尺度的测度。 

 

 

图12 一个系统可能在多个不同状态保持居于稳定。推动系统在景观中移动的干扰和改变景观形态的缓慢的系统变化均可驱动系统在状态间的移动。一个状态的稳定性是一个局部的测度，它取决于在当前位置景观的坡度。而一个状态的可塑性是一个大尺度的测度，因为它对应于系统现在所处凹陷的宽度（引自Peterson et al. 1998） 

  

六、生态可塑性—只不过是个隐喻？ 

   Carpenter等（2001）批评道，长期以来，可塑性被用于表达不同的意思：与可持续性相关的隐喻，动态模型的特性，在社会生态系统的实地评估研究中能被测量的数量，但是关于量化可塑性的可操作的指标几乎未被关注。 

1.可塑性的概念性度量 

一般将吸引域的容积（size of the attraction basin）作为Holling（1996）定义的生态可塑性大小的度量，从二维的稳定性景观图来看，这取决于波谷的深度和宽度。Scheffer等（2001）认为如果吸引域的容积越小，则可塑性也越低，甚至一个中等程度的扰动就可能使系统进入另一个吸引域。van Nes和Scheffer（2007）用图13（A，B）直观地表示可塑性的大小，而从小的扰动的恢复速率是局域稳定性的度量图13（C, D）。 

  

 

 

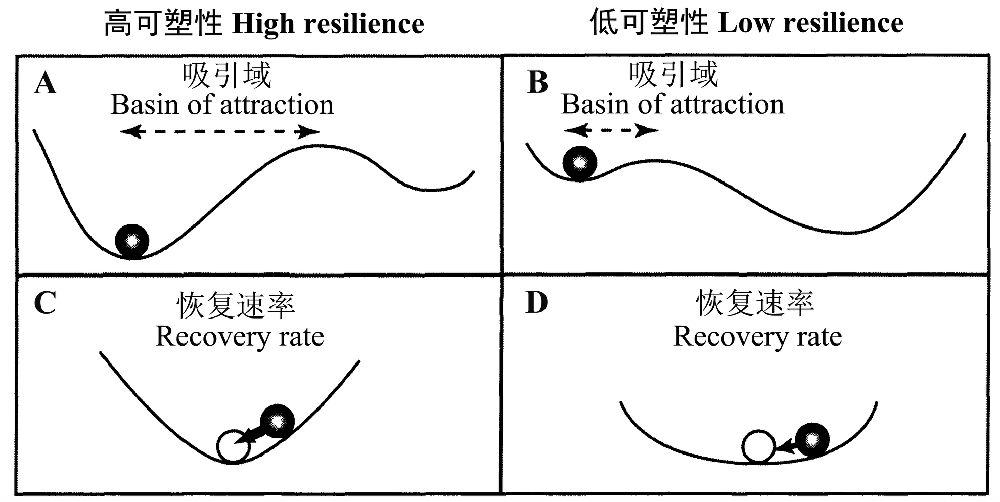
图13 通过在有波峰和波谷的稳定性景观中球的命运来直观地表述不同的生态可塑性（引自van Nes and Scheffer 2007） 

  

Walker等（2004）提出用4个要素来刻画可塑性：1）宽度（Latitude）：指一个系统在不丧失恢复能力（未越过阈值，如果突破了阈值，系统建难以甚至不能恢复）的条件下能被改变的最大量；2）阻力（Resistance）：指系统被改变的难易程度；3. 不稳定性（Precariousness）：指系统现在的状态离极限或阈值有多近；4. 组织形式（Panarchy）：因为跨尺度相互作用，在某个特定聚焦尺度的可塑性将同时受到上下尺度的状态和动态的影响。他们将吸引域中的宽度、阻力和不稳定性进行了图解（图14），可以认为它们试图对Holling（1973）可塑性概念的细化与形象化，但从本质上来看，仅是图13的一种扩展。他们并未解释如何定量这些参数，从本质上来说还是停留于概念的定性描述。 

 

图14 一个三维的稳定性景观图，有2个吸引域，在一个域内标示了系统现在的位置以及决定可塑性的三个参数，L=宽容度，R=阻力，Pr=不稳定性（引自Walker et al. 2004） 

  

Walker等（2004）以草原生态系统为例给予了说明，即这一稳定性景观有二个吸引域，一个为原始的（如许多牧草、灌木稀少、很多牲畜）稳态，另一个为退化的（如牧草稀少、灌木丛生、很少牲畜）稳态。人们的目的就是为了防止系统从原始的稳态进入困难或难以恢复的退化稳态。如果退化的吸引域深而陡（阻力值R较大），则需要更大的干扰或管理努力去改变系统的状态或稳定性景观。 

2.可塑性的半定量 

Carpenter等（2001）以湖泊生态系统为例，尝试了一种半定量的方法。将湖泊区分为二种稳态：一种为低磷、慢循环和好水质，另一种是高P、快循环和差水质。以快变化变量（水中P）为纵轴、以慢变化变量（沉积物P）为横轴来图示系统平衡，以此度量可塑性（图15）。 

因为有多个稳态，因此必须确定考虑哪个特定的稳态，此处，选择关注清水状态的可塑性。图15中的垂线将清水状态的可塑性界定成3个区，在最左区，清水态可塑性无穷大，在最右区，系统从任何位置都将进入浊水态，清水稳态的可塑性为零。在中间区，如果起始点位于不稳定线下方，系统将进入清水态，反之将进入浊水态。 

Carpenter等（2001）定义清水态的可塑性为不稳定平衡到清水平衡之间的距离，一个大于这一数量的P增加的干扰会使系统进入浊水态吸引域。此外，其它变化更慢的变数（譬如流域土壤的背景P浓度）也会影响清水态吸引域的可塑性：如果土壤P极低，曲线将伸直到浊水态吸引域消失，如果土壤P极高，曲线将抬起到在所有沉积物P水平下清水态可塑性均为零。 

 

 

图15 水中磷与沉积物磷之间的关系—清水状态的平衡和可塑性。箭头表示不稳定与清水吸引域之间的距离。垂直虚线表示其中一种稳态的可塑性变为了零（引自Carpenter et al. 2001） 

  

   图15的参数是可以具体化的，因此，以这种方式对可塑性的度量应该可以称得上半定量。虽然这也会面临一些不确定的困难，如影响水质的因素除了P还有N，还会受到气候变化的影响，沉积物—水界面还存在着复杂的N、P交换过程，等等。 

van Nes和Scheffer（2007）通过模型研究认为系统从小扰动的恢复速率（这有时被称为工程可塑性engineering resilience）是生态可塑性的一个很好的指标。这样的恢复速率随着灾难性的稳态转化的临近而降低，这种现象在物理学中被称为临界松弛（critical slowing down）。他们在所用的6种生态模型中都观察到这种现象的发生，并且都离稳态转化的阈值足够远，因此在实践上可能可以用于系统灾变的早期预警。图16是根据May（1977）的模型（牧食以逻辑斯蒂方程增长的种群X，环境容量K=10）进行模拟研究的结果。 

van Nes和Scheffer（2007）实际上在讨论系统在稳定性景观的特定吸引域内的行为，有些类似Walker等（2004）描述的不稳定性（图14中的Pr）。 

 

 

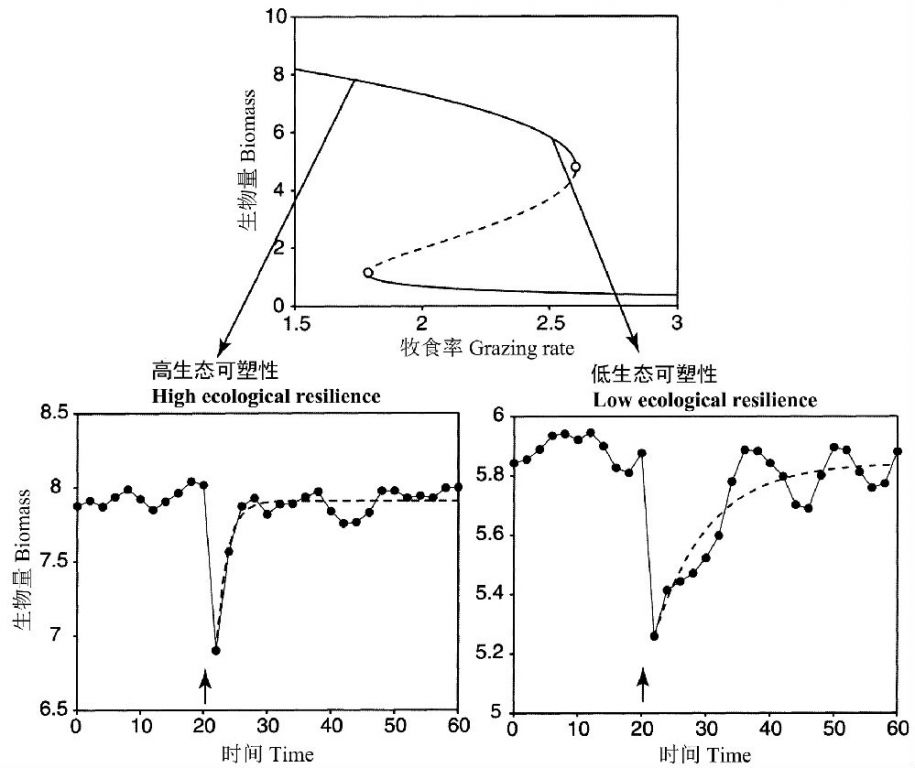
图16 利用May（1977）的模型模拟的瞬时扰动实验，在二种情形，扰动导致10%的生物量下降（垂直箭头）（引自van Nes and Scheffer 2007） 

  

 

3.可塑性也会变化 

很显然，依据可塑性的定义及图解，稳定性景观的变化将会导致生态可塑性的变化。Walker等（2004）认为外界的驱动因素（降雨、交换速率）和内部的过程（植物演替、捕食者—猎物周期、管理实践）能导致稳定性景观的变化，如吸引域数目的变化、域在状态空间中位置的变化、域之间阈值（边缘）位置的变化（图14中的L）或域“深度”的变化。比较图14和图17，可见稳定性景观的变化。 

 

 

图17 稳定性景观的变化引起了系统所在的域的萎缩以及另一个域的扩张。如果稳定性景观没有发生变化，系统可能变换了域（引自Walker et al. 2004） 

  

七、生态系统的稳态转化与时滞 

发育的阶段性是生命系统的共有特性，它广泛存在于不同层次的生命系统，譬如在生物个体水平，全变态昆虫的一生需经历形态完全不同的四个发育阶段（卵→幼虫→蛹→成虫），这里会飞的成虫与只能爬行的幼虫、不会动的蛹相比，真是有天壤之别！很多生态系统的发育也会呈现阶段性，譬如在第6章将要介绍的植物群落的演替，正是生态系统发育阶段性的真实写照。没有生态系统发育的阶段性，就没有任何相对稳定的暂态，也就不可能有所谓的稳态转化。从另一种角度来看，稳态转化也是昭示着一种从量变到质变的生态系统突变过程。 

1.生态系统对环境变化的响应—从渐变到突变 

一些智慧的理论生态学家擅长于把复杂的问题简单化，大胆的提出高度简化但却又能符合常识的模式。相比之下，很多专业的生态学家往往满脑子填充着复杂的关系与相互作用，不情愿或索性不知道如何大刀阔斧地去简化自然界。 

生态系统状态对环境变化的响应模式是理论生态学家复杂问题简单化的一个切入点。Scheffer等（1990，2001）提出了生态系统对环境条件变化（如各种胁迫—气候变化、营养盐输入、有毒化学物污染、地下水减少、生境破碎化、物种多样性丧失等）响应的三种可能模式： 

1）生态系统状态呈现平稳的逐渐变化过程（图18a）； 

2）生态系统状态在一定范围内响应相当迟缓，而接近某一临界水平时强烈地响应，形成突变（图18b）； 

3）当生态系统的响应曲线向回“折叠”时便出现一种完全不同的情形，即在同样的环境条件下，生态系统可存在于两种不同的稳定状态之中，被一个不稳定的平衡区（它显示了这二种状态吸引域之间的边界）隔开（图18c）。 

从某种意义上看，图18c也是稳定性景观的一种表现形式，它以生态系统状态对环境条件的响应轨迹为基础，而在图4-2中描述的稳定性则是以二个种群的相互作用轨迹为基础。 

 

 

  

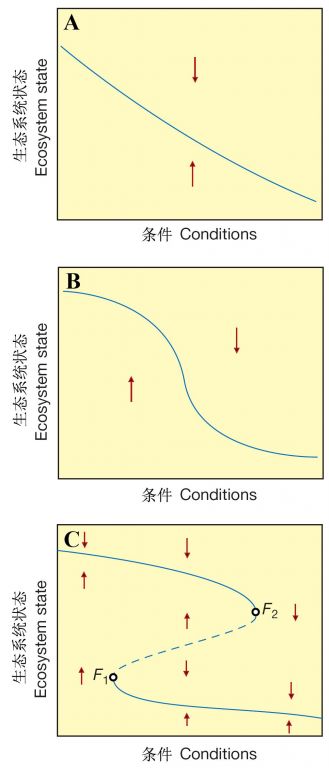
图18 生态系统状态随环境条件（如营养盐负荷、开采或温度上升）改变而变化的可能方式。在A和B中，每个条件只有一个平衡存在；但是如果平衡曲线向回折叠（C），对某一条件可能存在三个平衡，从箭头（表示变化的方向）可见，在中段虚线处的平衡是不稳定的，代表了上下二个分支所处的稳态吸引域的边界（引自Scheffer et al. 2001） 

  

地学的证据也表明在数千年或更长的时间尺度上气候变动导致生态系统状态出现突变（图18b）。譬如，撒哈拉地区的植被，在围绕一个逐渐下降的趋势震荡了很长一段时期以后，在距今约五千多年前，由于非洲湿润期（African Humid Period）的突然结束而突然崩溃变成了沙漠（deMenocal et al. 2000）（图19）。 

 

 

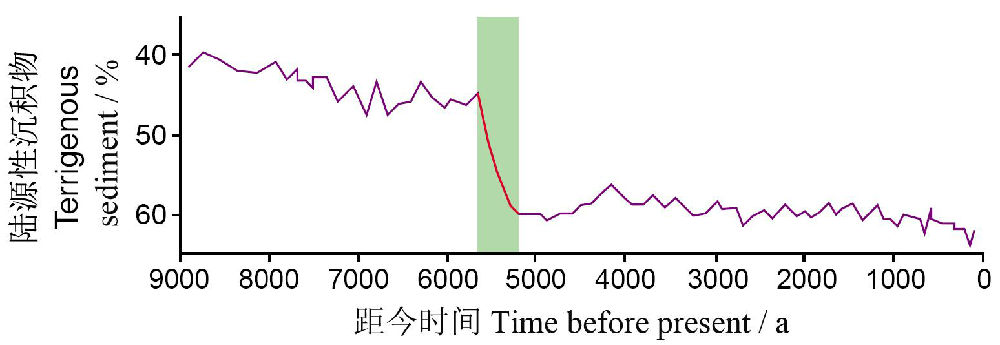
图19 撒哈拉植被的崩溃—古老的稳态转化的案例。在围绕着一个平稳的下降趋势震荡了数千年之后，撒哈拉的植被在5000-6000年以前突然崩溃，这反应在陆源性尘土（坐标轴逆转了）对靠近非洲海岸的一个海洋沉积物样点的贡献上（引自deMenocal et al. 2000，Scheffer and Carpenter 2003） 

  

2.生态系统的稳态转化—从实践到理论 

   稳态转化概念是从人们对自然生态系统存在多暂态平衡的直观认识中抽象出来的。一般来说，自然界的生态系统都会具有两个或更多的可交替（或可转化）的稳定状态。譬如，在浅水湖泊中，水生高等植物占优势的清水状态和浮游藻类占优势的浊水状态便是生态系统多稳态的很好的例子（图20）。 

 

 

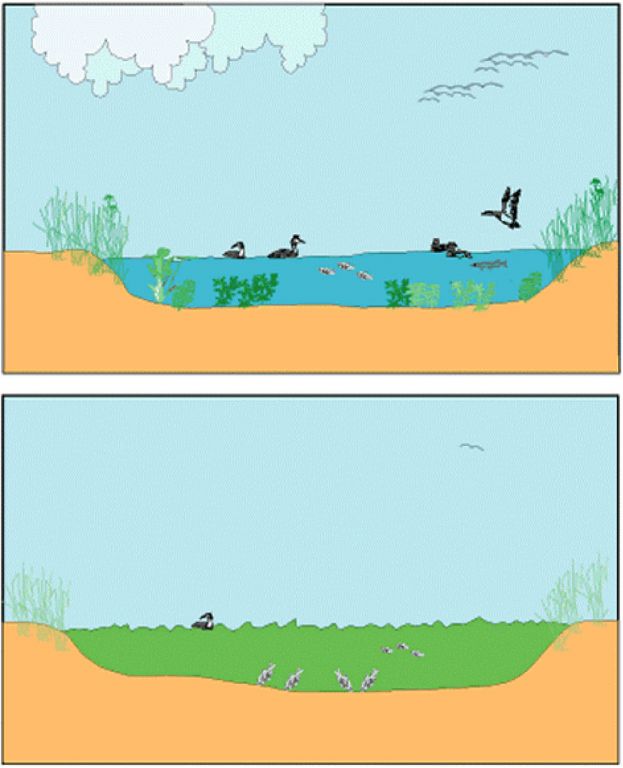
图20 一个水生高等植物占优势的清水状态（上图）和一个因沉水植物大量衰退、鱼类和风浪搅拌底泥、浮游植物占优势的浊水状态的浅水湖泊示意图（引自Scheffer 2001） 

  

Scheffer（1990）从理论上分析了浅水湖泊中的营养盐水平—浊度—水生植被的相互作用轨迹，图示了浅水湖泊中二种稳定状态（清水稳态 vs 浊水稳态）之间的相互转化（图21），基于三个经验事实：1）湖水的浊度随营养盐水平的增加而增加，2）沉水植被降低浊度，3）当浊度超过某一临界点时，沉水植被消失。浊度和营养水平之间存在二种不同的函数关系，一种是水生植被占优势的情形，另一种是无植被的情形。在较低的营养盐水平下，只有植被占优势的平衡存在，而在较高的营养盐水平，仅有无植被的平衡存在。在一个中间的营养盐范围内，二种平衡都存在：一种有植被，而另一种较混浊而无植被，它们被一个不稳定的平衡（虚线）所隔开。 

 

 

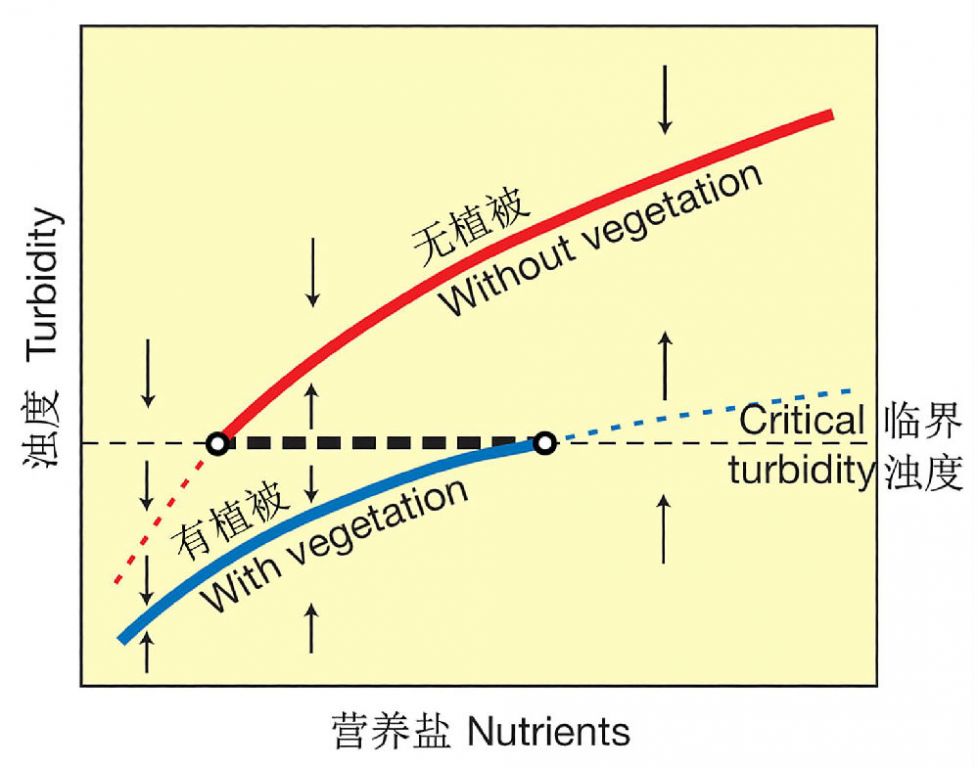
图21 浅水湖泊中二种稳定状态转化模型的图解（引自Scheffer et al. 2001） 

  

在海洋生态系统中，也存在一些可交替的生态系统状况（图22）：（A）为热带珊瑚礁：①显示1979年在加勒比海，群落由鹿角珊瑚（Acroporapalmata）和鹿角轴孔珊瑚（Acroporacervicornis）占优势，②显示20多年以后，同一礁，退化并被肉质的海草—网地藻（Dictyota spp）所覆盖；（B）为温带和北方岩礁：①显示在阿留申群岛，海带占优势的系统（Alariafistulosa），②显示被过度牧食的海胆Strongylocentrotuspolycanthus荒地，（C）为温带海岸远洋系统：①显示肉食性鱼类Scombrus scombrus，②显示过度捕捞而枯竭的食物链，被食浮游生物的水母Aurelia aurita占据优势。这样的例子在世界各地举不胜数（Hughes等2005）。 

 

 

图22 海洋生态系统可交替的生态系统状况的三个例子（引自Hughes et al. 2005） 

  

Folke（等2004）用稳定性景观变化图示了自然界中存在的各种不同生态系统中稳态转化的例子（表2）。人类在过去的历史时期，特别是在工业革命之后，对自然生态系统产生了强烈的影响，通过下行（如顶级捕食者的过度捕猎）和上行（如增加营养盐通量）影响，或通过认为的干预（如防止草地和森林火烧），还有由于全球气候的变化（如变暖引起的珊瑚礁白化），显著改变了生态系统应对变化的能力。这些综合影响的结果是使生态系统趋向于耗散（leaking）、简化（simplified）和“杂草化（weedy）”，并伴随着不可预测且往往令人惊讶的生态系统服务功能的改变。 

  

表2 各种各样的生态系统状态交替（1、4）及其原因（2）和触发因素（3）（引自Folke et al. 2004） 

清水型湖泊  Clear  water lakes	农田和湖泊底泥中P累积	洪水、气候变暖、过度捕杀捕食者	浊水型湖泊  Turbid  water lakes
珊瑚礁  Coral-dominated  reefs	过度捕捞，海岸带富营养化	病害、白化、飓风	藻占优势的礁  Algae-dominated  reefs
草地 Grassland	防火	多雨，持续的强度牧食	灌丛草地  Shrub-bushland
草地 Grassland	猎杀牧食者	病害	林地Woodland
海藻森林  Kelp  forests	顶级捕食者的功能性灭绝	过热事件、暴风、病害	海胆占优势  Sea  urchin dominance
Pine  forests 松树林	微气候和土壤变化，松树更新能力丧失	火烧频率下降、火烧强度增加	橡树森林 Oak forest
海草场  Seagrass beds	移去牧食者，缺乏飓风，盐度变化，空间同质化	过热事件	浮游植物水华  Phytoplankyon  blooms
有沉水植被的热带湖泊  Tropical  lake with submerged vegetation	干旱期间营养累积	伴随地下水位上升的营养盐释放	漂浮植物占优势  Floating  plant dominance

  

Scheffer（1990，2001）用三维图形象地表示了生态系统稳定状态之间的转化，将一个“杯中弹子”（Marble-in-a-cup）图叠加在图18c上（图23）。这一稳定性景观刻画了在五个不同条件（如营养盐水平）下的生态系统的状态（如浊度）及其吸引域。稳定平衡对应于波谷，而折叠的位于中段的不稳定平衡对应于波峰。如果吸引域的容积较小，即使一个中等程度的扰动都有可能将系统推进到另一个吸引域中去。 

如果仔细琢磨一下，可将Sheffer（1990）的这个“杯中弹子”图看成是Holling（1973）所描绘的轨迹在势场上的移动图（图3）的一个扩展。值得称赞的是，Sheffer（1990）还将其叠加在一个相平面图上了。 

  

 

 

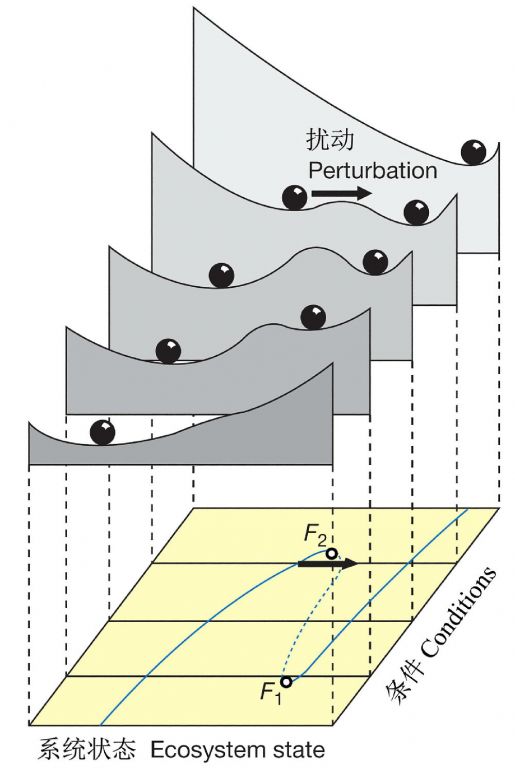
图23 “杯中弹子”图示五个不同状态生态系统的稳定状态。波谷对应稳定状态，波峰对应于转折点（引自Scheffer et al. 2001） 

  

3.时滞—下降与回复的轨迹不同 

生态系统稳态转化之中出现的一个特殊现象就是所谓的时滞。根据维基百科（Wikipedia）的解释，时滞hysteresis源自古希腊语ὑστέρησις，意指缺陷（deficiency）或滞后（lagging behind）。时滞指系统可能呈现出路径依赖性（path dependence）或非速率依赖性记忆（rate-independent memory）。在许多生态系统的稳态转化过程中，呈现不同程度的时滞现象，即它们的恢复与其下降时的轨迹不同。 

Beisner等（2003）提出时滞现象的产生主要是由于扰动引起决定稳定性景观形状的参数的变化所致（图24），因此一个扰动使系统向前进入另一个新的状态，但同样大小的扰动却无法使其反方向返回原来的状态。其实，这种变化在Scheffer（2001）的论文的图中（图23）中已有清晰的描绘。 

 

 

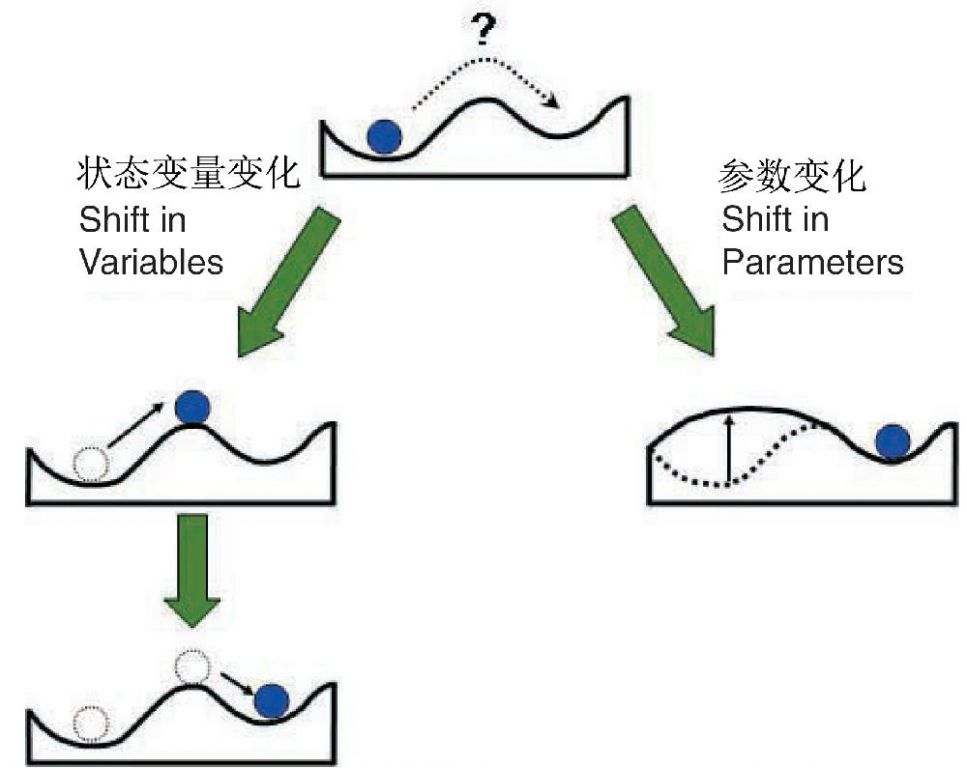
图24 二维“杯中弹子”图显示：状态变量变化（由于扰动）导致球（系统）的移动（左图），参数变化导致稳定性景观自身的变化，其结果是球被移动到另一个状态，但同样大小但方向相反的扰动却无法使球回到原来的位置（右图）（引自Beisner et al. 2003） 

  

Meijer（2000）给出了一个稳态转化过程中出现时滞的经典的研究案例。在浅水的Veluwe湖中，轮藻植被对磷浓度增加和随后的降低响应过程中出现了时滞现象，即轮藻恢复的营养盐水平要比轮藻崩溃时要高得多（图25）。为何会出现这种水生植物难以恢复的时滞现象？可能的原因有种群补充受阻（种子库减小）、草食性鱼类的过度牧食（特别是对幼芽）、有毒污染物的积累以及有毒藻类的化感作用等。 

 

 

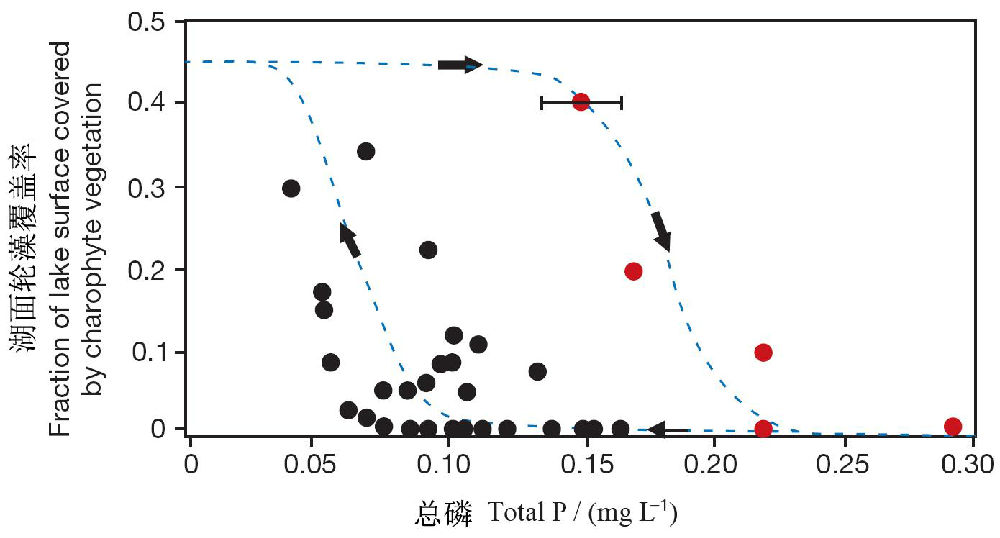
图25 浅水湖泊—Veluwe湖的轮藻植被对磷浓度增加和随后的降低响应过程中出现的时滞。红点表示20世纪60年代后期至七十年代初之间向前转换的年份，黑点表示90年代营养盐逐渐降低最终导致向回转换的效应（引自Meijer 2000） 

  

Suding等（2004）概念性地分析了放牧压力对牧场植被稳态转换的影响。当牧食压力从E1增加到E2时，牧场可能还能维持在生态系统状态S₁（图26A中沿曲线线的绿色区域），可是当牧食压力超过E₂后，系统将崩溃到一个灌木占优势的退化系统（S₂），因为已经超过了一个临界点。一旦系统崩溃到S₂，将不会恢复或回到草地状态（S₁），除非牧食压力（或其它因素）减少到E₁。与系统的崩溃（图26B）相比，这一恢复过程将是昂贵而缓慢的，并依赖于反馈作用，可能完全不能恢复。干扰（自然的或人为的）能更直接地影响返回轨迹，譬如，通过管理上的努力（如移去灌木）去影响状态变量（图26B，双线箭头），可能使系统不必降低环境条件到E₁以下就能返回到S₁。 

 

 

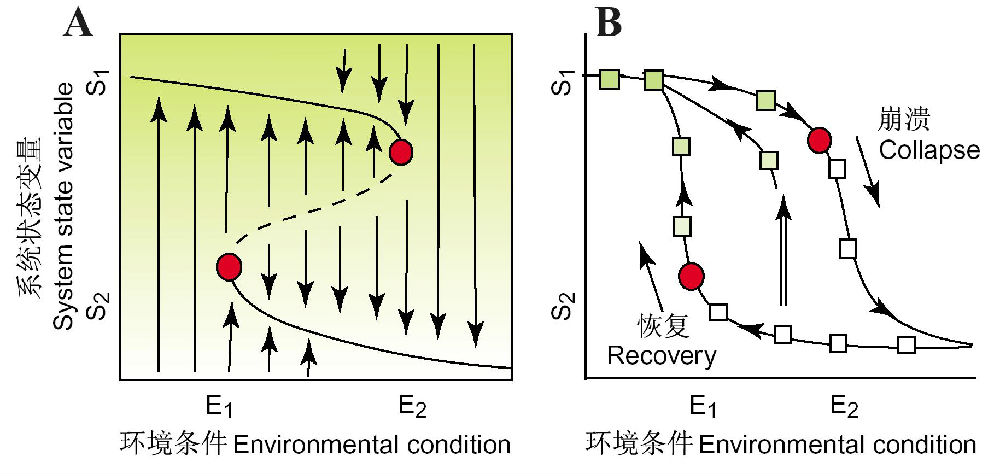
图26 可替换状态模型与生态恢复（引自Suding et al. 2004） 

  

4.减轻或避免时滞—现代生态系统管理策略的战略转变 

1）在受损生态系统的修复过程中，如何降低时滞的效应？ 

具有时滞特征的稳态转化对受损生态系统的自然恢复或认为修复往往产生明显的影响。譬如，在过去的半个多世纪中，在强烈的人类活动（如持续的N、P输入）干扰下，我国东部区域许多浅水湖泊中的优势生物类群—水生维管束植物（也有水下森林之称）大量衰退甚至绝迹，水质恶化。从稳态转换的观点来看，表征系统状态的主要参数（如N、P）已经超越了新的系统状态或吸引域（如浊水）的阈值。一方面，在流域人口不断增加的情况下，外源N、P负荷难以削减，对系统状态变量的修复异常艰难。另一方面，倾尽数十年的各种努力，仍无法有效恢复曾经占据优势的原始（或原生）水生植物群落。在一些湖泊（如武汉东湖），虽然N、P水平有了很大改善，强烈的时滞效应依然顽强地阻止着植被的自然恢复。 

让我们从生态学角度来分析时滞产生的主要机理。若在一个湖泊中水生植物群落消失已有数十年之久的话，沉积物中的植物种子库可能已经大量衰减甚至消失，此外，在一些极端情况下，厌氧的沉积物已很难再适合一般的水生植物的生长。再加上人为的水文调控，失去了适合水生植物生长的自然的水文节律，也失去了与外界水体有效的种源交换，因此，植物群落恢复出现严重的时滞一点都不足为奇。 

在很多情况下，时滞的程度可能与水生植物种子库的资源量成负相关，与沉积物的厌氧状态呈正相关。因此，在对这类湖泊进行水生植被恢复或重建过程中，种源的补充或基底的改造可能是减缓或消除时滞的重要举措。所谓人为的生态修复实质上就是为了改变退化生态系统的返回轨迹。 

2）优先“保健”还是优先“治疗”？ 

具有时滞特征的稳态转化对管理产生的影响也十分深远：维护一个良性的生态系统比修复一个状态已转变了的系统是否更加容易？或者说是否耗费更少的金钱？这是一个需要用事实回答的问题。基于时滞现象的存在，许多学者认为忽视稳态转化的可能性将使社会付出沉重的代价（Scheffer et al. 2001；Hughes et al. 2005）。 

在公共医学领域，人们是不会质疑维护人的健康比生病后治理更为有效的理念的。我国目前的湖泊富营养化治理策略似乎正在推崇一种类似的理念—维护一个良性的生态系统比修复一个受损的系统更加有效。在过去的几十年中，我国湖泊治理的重心一直放在富营养化严重的三湖—滇池、太湖和巢湖，这三个湖泊早已从清水稳态进入到浊水稳态，蓝藻水华连年大规模暴发，虽耗费巨资进行治理但却收效甚微。近年来，国家环镜保护部开始大力推动生态系统状态良好湖泊（如湖北梁子湖等）或富营养化初期湖泊（如云南洱海等）的生态环境保护或防退化计划，或许是为了减少时滞社会代价的一种管理与工程举措。 

  

结语 

如何刻画生态系统状态与行为？主要通过稳定性、可塑性及稳态转化等，虽然停留于定性或半定量。这类研究几乎仅涉及到一些中短时空尺度的生态过程，优点是可服务于人类的生态系统管理策略，譬如，在受损生态系统的修复过程中，如何降低时滞效应在管理上具有意义。 

遗憾的是，这些概念并未有效地向其它领域扩展，这种从量变到质变的多状态现象在自然界中普遍存在。譬如，物种进化中变异积累到一定程度就能跃变为新物种，植被的序列演替就可看成是不同稳态间的转化，等等。 

如何将这些系统特性扩展到地史尺度的生态过程依然面临着不小的困难与挑战，因为时间尺度几乎成比例地交织于空间尺度之中，而这不可避免地遭受最难预测、最难重复以及最具随机性的气候与地质运动的驱动。即便如此，如何跨尺度地审视生命系统的状态、行为与动态从而揭示不同层次以及整个生命系统的运作与演化规律是未来生命科学面临的重要挑战之一。 

  

参考：从生态学透视生命系统的设计、运作与演化—生态、遗传和进化通过生殖的融合（谢平著，科学出版社，2013）